Глава пятая. МЕХАНИКА ТЕЛЕСКОПА

§ 1. НЕБЕСНАЯ СФЕРА И СИСТЕМЫ НЕБЕСНЫХ КООРДИНАТ

Прежде чем перейти к описанию монтировок телескопов, необходимо кратко рассказать о небесных координатах.

Небесная сфера - воображаемая поверхность, не имеющая определенного радиуса. Мы видим эту сферу изнутри, и ее центр находится точно там, где расположен наблюдатель.

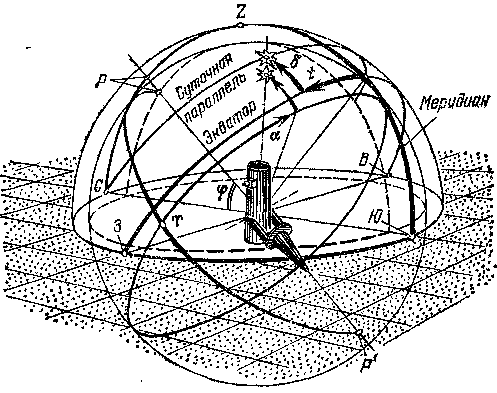
Рассмотрим основные точки и круги небесной сферы (рис. 83), для чего выделим из двух сфер, изображенных на рисунке, наружную. Точки пересечения воображаемой оси вращения небесной сферы с самой сферой называются полюсами. Северный полюс мира (Р) виден в северном полушарии Земли, южный (Р') - в южном. Близ Северного полюса расположена Полярная звезда. Близ Южного нет сколько-нибудь заметной звезды.

Рис. 83. Подвижная и неподвижная системы координат. Неподвижная система нанесена на наружную сферу, подвижная - на внутреннюю. Меридиан и горизонт, не участвующие в суточном вращении, показаны шгриховой линией

Высоту полюса мира над горизонтом можно измерять в градусах, она равна географической широте места наблюдений (f).

Большой круг сферы, проходящий через точку севера (С), полюс (Р), зенит (Z) и точку юга (Ю), называется небесным меридианом. Меридиан делит небо-на два полушария - восточное и западное.

Линия пересечения плоскости земного экватора с небесной сферой называется небесным экватором. Каждая точка экватора удалена от полюса на 90°. Малые круги, плоскости которых параллельны плоскости экватора и вдоль которых происходит суточное движение светил, называючся суточными параллелями.

Экватор проходит через точки востока (В) и запада (3). В южной части неба он максимально поднимается над горизонтом. Точка пересечения экватора с меридианом поднимается над горизонтом на высоту 90° - f, где f - географическая широта места наблюдений.

Для уверенного поиска светил, особенно слабых и невидимых невооруженным глазом, созданы системы небесных координат. Мы рассмотрим только две из них - неподвижную (первую) экваториальную (наружная сфера на рис. 86) и подвижную (вторую) экваториальную (внутренняя сфера). Разделение сферы на две - условное, нужное для того, чтобы яснее различать обе системы.

В обеих системах координат одна координата общая. Эта координата указывает кратчайшее на небесной сфере расстояние светила от небесного экватора. Она называется Склонением светила (d).

Если светило лежит на экваторе, его склонение равно 0 . Склонение северного полюса +90°, южного - 90°. Склонение звезды Денеб (a Лебедя) равно 44°55', склонение звезды Ригель (b Ориона) равно - 8°19'.

Вторая координата в каждой системе своя. В первой системе (наружная сфера на рис. 86) - это часовой угол (t). Часовой угол измеряется от меридиана до светила. По мере вращения небесной сферы часовой угол светила непрерывно меняется, поэтому его удобно измерять в часах, минутах и секундах (ч, м, с или латинскими буквами h, m, s) от меридиана по ходу вращения небесной сферы (по часовой стрелке). Каждый час часового угла равен 15° в угловой мере. Предположим, сейчас меридиан пересекает Капелла (a Возничего), и ее часовой угол равен нулю. Через час часовой угол Капеллы станет 1^h (15°), еще через полтора часа 2^h30^m (37,5°). Эта система удобна для снабжения телескопа координатным кругом по часовому углу, но неудобна для составления каталогов и звездных атласов. Для каталогов принята вторая (подвижная) система координат (внутренняя сфера на рис. 83). Склонение здесь определяется так же, как и в первой системе, а вместо часового угла служит прямое восхождение (а), которое отсчитывается от так называемой точки весеннего равноденствия () до светила против вращения небесной сферы (против часовой стрелки). Так как точка весеннего равноденствия () участвует в суточном вращении небесной сферы, вся система координат оказывается подвижной относительно наблюдателя, но неподвижной относительно звезд. Прямое восхождение отсчитывается также в часах, минутах и секундах. Если в данный момент меридиан пересекает светило с прямым восхождением a=0^ч 0^м, то час спустя его пересечет светило с a=1^ч 0^м.

Время полного оборота Земли относительно звезд - звездные сутки - на 4 минуты короче солнечных суток, по которым мы живем. Дело в том, что благодаря обращению Земли вокруг Солнца мы видим как оно ото дня ко дню перемещается среди созвездий. Конечно, днем звезды не видны, но зато по ночам вид звездного неба меняется в течение года. Каждые сутки Солнце в своем видимом годовом движении смещается на небесной сфере на 1° к востоку в том же направлении, что и Земля в своем суточном вращении. В результате солнечные сутки на 4 мин длиннее звездных.

Мы живем по солнечному времени, но телескоп приходится поворачивать за звездами по звездному времени со скоростью один оборот в звездные сутки. Это вынуждает нас вычислять звездное время по известному солнечному, чтобы найти часовой угол светила.

Интересно, что звездные сутки начинаются в тот момент, когда меридиан пересекает (кульминирует) точка весеннего равноденствия c a=0^ч. Выходит, что звездное время в любой момент суток в точности равно прямому восхождению светил, которые в это время кульминируют. Например, если в какой-то момент кульминирует Вега (a Лиры), прямое восхождение которой a=18^ч 34^м, то звездное время также равно 18^ч 34^м. Планетарная туманность «Гантель» (М 27) в созвездии Лисички всегда кульминирует в 19^ч 54,7^м звездного времени, так как ее a=19^ч 54,7^м.

Таким образом, взглянув на часы, идущие по звездному времени, мы можем сразу узнать прямое восхождение светил, кульминирующих в данный момент.

Предположим, что сейчас 5 ^ч звездного времени. Нам нужно найти слабую галактику с a=3^ч Ясно, что кульминировала она 2 часа тому назад. Значит, нам нужно повернуть телескоп к западу от меридиана на угол 2^ч (в угловой мере на 30°). Но этому соответствует часовой угол t=2^ч. Установив на круге часовых углов 2, а на круге склонений склонение этой галактики, мы приведем ее в поле зрения телескопа без помощи искателя. Для слабых объектов, не видимых в искатель, это наиболее надежный и простой способ поиска объектов.

Каждая любительская обсерватория должна быть снабжена часами, идущими по звездному времени. Это могут быть обычные часы, которые спешат на 4 мин в сутки. Часовой угол вычисляется по формуле

t=S₀-a,

где S₀ - звездное время на гринвичском меридиане в 0^ч всемирного времени (см. в Переменной части Астрономического календаря раздел «О счете времени» и последнюю колонку в эфемеридах Солнца). Там же можно прочесть о переводе декретного и летнего времени в звездное. После длительного перерыва в наблюдениях, если звездные часы остановились, достаточно привести в поле зрения телескопа объект, прямое восхождение которого известно, и, определив часовой угол по соответствующему кругу телескопа, определить гринвичское звездное время и пустить часы.